Скремблирование
Перед записью на диск, содержимое сектора в обязательном порядке подвергается скремблированию (от английского scrambling —– перемешивание), – т. е. преобразуются в псевдослучайную последовательность, близкую по своим характеристикам к "белому шуму", что исключает непреднамеренное образование регулярных последовательностей с высоким значением DSV —– такие последовательности с точки зрения считывающего устройства считаются крайне неблагоприятными и читаются весьма нестабильно (подробнее об этом см. разд. "Синхрогруппы, объединяющие биты и DSVСинхрогруппы, merging bits и DSV" этой главы).
СкремблируетсяСкремблируются все поля сектора, кроме 12-байтовой синхрогруппы в его начале (если скремблировать и синхрогруппу, то – как потом ее прикажете находить в потоке данных?), что в совокупности составляет 2340 байт данных (см. рис. 1.15 0х045).

Рис. 1.15. унок 15 0х045 Формат сектора с точки зрения скремблера
Скремблирование осуществляется записывающим приводом на аппаратном уровне и совершенно незаметно для программиста. Соответственно, при чтении сектора выполняется обратная процедура, т. е. происходит "скремблирование наоборот" или "де-скремблирование", в процессе чего сектор очищается от "белого шума" и преобразуется к своему исходному виду.
Прозрачность механизма скремблирования создает обманчивое впечатление, что значение его алгоритма совершенно бесполезно для программиста и представляет интерес лишь для разработчиковм аппаратуры. На самом же деле это не так. Коль скоро скремблер для того и придуман, чтобы исключить непреднамеренное появление неблагоприятных последовательностей, то стало быть умение умышленно формировать такие последовательности умышленно
создавать, позволяет создавать диски нечитаемые на аппаратном уровне. Тоже мне новость! —– хмыкнете вы. Создать нечитаемый диск —– много ума не надо. Вжик циркулем по отражающему слою и "родная мама его не узнает".
А еще есть пресс-папье и просто кувалда. Шутки шутками, но весь фокус в том, что благодаря наличию корректирующих кодов можно создать неблагоприятную последовательность, вычислить соответствующие ей корректирующие коды и в слегка измененном виде изменить записать эту последовательность на диск так, чтобы с одной стороны она из неблагоприятной превратилась в благоприятную, а с другой —– при прохождении сквозь декодер Рида-Соломона восстанавливать в свой исходный —– неблагоприятный вид. Попытка скопировать такой диск штатным копировщиком ни к чему хорошему не приведет, т. к. он запишет неблагоприятную последовательность в том виде как она есть, и при ее чтении которой наверняка произойдет ошибка! Захватывающая перспектива, не правда ли? Подробнее об этом приеме мы поговорим в главе 6 , а пока же сосредоточимся на скремблере.
Алгоритм скремблирования, согласно стандарту ECMA-130, выглядит так: "Each bit in the input stream of the scrambler is added modulo 2 to the least significant bit of a maximum length register. The least significant bit of each byte comes first in the input stream. The 15-bit register is of the parallel block synchronized type, and fed back according to polynomial x15 + x + 1. After the Sync of the Sector, the register is pre-set with the value 0000 0000 0000 0001, where the ONE is the least significant bit" ("Каждый бит входного потока скремблера суммируется по модулю 2 с наименее значимым битом максимальной длины регистра. Наименее значимый бит каждого байта, проходит первым во входном потоке. 15-битный регистр представляет собой параллельный блок синхронизированного типа, и заполняется в соответствии с полиномом x15 + x + 1. После прохождения синхрогруппы сектора, – которая не скремблируется, – регистр инициализируется значением 0000.0000.000.0001, где ЕДИНИЦА есть наименее значимый бит" (, см. рис. 1.16 0x44).
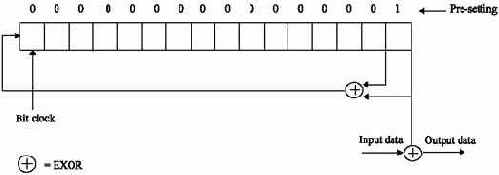
Рис. 1.16. унок 16 0х044 Блок схема скремблера
Листинг 1.1. Программная модель скремблера к рис. 1.16
UpdateShiftRegister()
{
int i;
for(i = 0; i < 8;i++)
{
int hibit = ((ShiftRegister & 1)^((ShiftRegister & 2)>>1)) << 15;
ShiftRegister = (hibit | ShiftRegister) >> 1;
}
}
void Scramble()
{
int i;
for (i=12;i<2352;i++)
{
Scrambled[i] = Scrambled[i] ^ (ShiftRegister&0xFF);
UpdateShiftRegister();
}
}
Листинг 1 Программная модель скремблера к рис. 0x044
Непонятно? Мне тоже было непонятно…. во всяком случае до тех пор, пока я не взял в руки дизассемблер и не "распотрошил" копировщик дисков Clone CD. Как известно, программа [n2k40] Clone CD великолепно справляется с защитами, основанными на слабых секторах (см. ….), а раз так, то – он должен содержать в себе свой собственный скремблер.
Действительно, среди функций, экспортируемых динамической библиотекой ElbyECC.dll (входящей в состав Clone CD) обнаруживается однао [n2k41] очень любопытнаяое функцияимя: RawSrcambleSector, дизассемблерный листинг которойго выглядит следующим образом (листинг 1.2).так:
Листинг 1.2. Пример реализации алгоритма скремблирования, позаимствованный из Clone CD
.text:100020E0 RawScrambleSector proc near
.text:100020E0
.text:100020E0 arg_0 = dword ptr 4
.text:100020E0
.text:100020E0 mov eax, [esp+arg_0] ; загружаем переданный аргумент в EAX
.text:100020E4 mov ecx, offset ScrmblrTbl ; в ECX – указатель на ScrmblrTbl
.text:100020E9 add eax, 0Ch ; пропускаем 12 байт синхропослед.
.text:100020EC push esi ; сохраняем ESI
.text:100020ED push edi ; сохраняем EDI
.text:100020EE sub ecx, eax ; вычисляем дельту
.text:100020F0 mov edx, 249h ; 2340 / 4 скремблируемых байт
.text:100020F5
.text:100020F5 loc_100020F5: ; CODE XREF: RawScrambleSector+22vj
.text:100020F5 mov esi, [ecx+eax] ; взять очередной DWORD из таблицы
.text:100020F8 mov edi, [eax] ; взять очередное скремблируемое DWORD
.text:100020FA xor edi, esi ; ксорим
.text:100020FC mov [eax], ed ; записываем результат
.text:100020FE add eax, 4 ; следующий DWORD
.text:10002101 dec edx ; уменьшить счетчик
.text:10002102 jnz short loc_100020F5 ; мотать цикл
.text:10002104 pop edi ; восстанавливаем регистр EDI
.text:10002105 pop esi ; восстанавливаем регистр EDI
.text:10002106 retn ; возвращаемся из функции
.text:10002106 RawScrambleSector endp
Листинг 2 Пример реализации алгоритма скремблирования, позаимствованный из Clone CD
Анализ дизассемблерного листинга показывает, что громоздкой и ресурсоемкой "возне" с полиномом разработчики программы Clone CD[n2k42] предпочли быстрый табличный алгоритм, сводящийся к наложению на скремблируемый сектор псевдослучайной последовательности посредством операции XOR. Фактически, мы получили ни что иное, как "одноразовый блокнот" Вернама, длина "секретного" ключа которого равна длине скремблируемой части сектора (2340 байт для справки). Будучи переведенным на язык высокого уровня данный алгоритм будет выглядеть приблизительно так как это показано в листинге 1.3.:
Листинг 1.3. Пример реализации табличного алгоритма скремблирования на языке Си
RawScrambleSector (char *raw_sector)
{
int a;
DWORD *p;
DWORD *MyScramblerTable = (DWORD *) ScramblerTable;
p = (DWORD*)(raw_sector + 12);
for (a = 0; a < 2340 / 4; a++)
{
p[a] ^= MyScramblerTable[a];
}
}
Листинг 3 Пример реализации табличного алгоритма скремблирования на языке Си
Теперь Оостается разобраться лишь непосредственно с самой псевдослучайной последовательностью, первые восемь членов которой (выдранные[n2k44] полученные с помощью дизассемблераом из того же Clone CD) выглядят следующим образом (листинг 1.4). так:
Листинг 1.4. Первые восемь членов псевдослучайной последовательности, используемой для скремблирования сектора, полученные из копировщика CloneCD
dd 060008001h
dd 01E002800h
dd 006600880h
dd 081FE02A8h
dd 028606080h
dd 0889E1E28h
dd 0AAAE6668h
dd 0E0017FFCh
Листинг 4 Первые восемь членов псевдослучайно последовательности, используемой для скремблирования сектора, выдранные из Clone CD
Вся таблица слишком великавелика, для того чтобы быть приведенной здесь целиком (даже напечатанная самым мелким шрифтом, который только допускают санитарные нормыслужбы, она занимает целую страницу, —– свыше четырех тысяч знаков, которые очень трудно "перебить" с бумаги в компьютер, не допустив при этом ошибок). Поэтому, представляет интерес найти закономерность, которой связаны члены данной последовательности, и воссоздать алгоритм, вычисляющий все члены последовательности по первому из них. Эта маленькая программистская головоломка отнюдь не так сложна, какой кажется поначалу. Да, беглый взгляд на первые восемь членов псевдослучайной последовательности не обнаруживает и намека на их природу —– числа меняются хаотично и сильно смахивают на "пляшущих человечков" над которыми ломал голову Шерлок Холмс. Только частотный анализ в данном случае бесполезен и в "лоб" эту задачу не решить. Но ведь мы начинаем анализ отнюдь не на пустом месте! Во-первых, нам достоверно известно, что скремблирование осуществляется по 16-разрядным словам (разрядность регистра скремблера как раз и составляет 16 бит), а раз так, то и анализировать мы должны именно слова, а не двойные слова.
То, что выполнение операции XOR[n2k45] "ксоренье" идет 32- битными кусками ничего не меняет, ведь – она XOR побитовая операция и потому конкретная разрядность операндов никак не влияет на конечный результат! Во-вторых, анализ закономерностей выгоднее всего проводить на битовом уровне, т. к. именно на битовом уровне эта псевдослучайная последовательность и генерируются.
Следующий Скрипт
(script)[n2k46] , показанный в листинге 1.5, автоматически преобразует все элементы таблицы в 16-разрядные слова, отображаемые в двоичном виде. Запустите дизассемблер IDA Pro, нажиме <F2> и загрузите файл, содержащий этот скрипт. Затем, подогнав курсор к первому элементу таблицы, нажмите <Shift-F2> и введите следующую команду: x2bin(ScreenEA(), ScreenEA()+2340, 2). Комбинация <Ctrl-Enter> (в ранних версиях IDA Pro просто <Enter>) запустит скрипт на выполнение.:
Листинг 1.5. Скрипт на IDA-Си, преобразующий элементы таблицы в двоичный вид
// x_start - начальный адрес для преобразования
// x_len - кол-во байт для преобразования
// x_pow - кол-во байт в одном элементе
static x2bin(x_start, x_end, x_pow)
{
auto a,p;
for(p=x_start;;)
{
// преобразуем в элемент нужной разрядности
if (x_pow == 1) MakeByte(p); else if (x_pow == 2) MakeWord(p); else
if (x_pow == 4) MakeDword(p); else return 0;
// в двоичный вид
OpBinary(p, 0);
// след. элемент
p = p + x_pow;
// выход, если все уже сделано
if (p>x_end) break;
}
}
Листинг 5 Скрипт на IDA-Си, преобразующий элементы таблицы в двоичный вид. Запустите IDA, нажиме <F2> и загрузите файл, содержащий этот скрипт. Затем, подогнав курсор к первому элементу таблицы, нажмите <Shift-F2> и введите следующую команду "x2bin(ScreenEA(), ScreenEA()+2340, 2)".
Комбинация <Ctrl-Enter> ( в ранних версиях IDA просто <Enter>) запустит скрипт на выполнение.
"Обновленная" псевдослучайная последовательность скремблера должна выглядеть так как показано в листинге 1.6 (в немниже приведены 16 ее первых членов).:
Листинг 1.6. Псевдослучайная последовательность, записанная в виде 16-разрядных слов, отображаемых в двоичной нотации
dw 1000000000000001b
dw 0110000000000000b
dw 0010100000000000b
dw 0001111000000000b
dw 0000100010000000b
dw 0000011001100000b
dw 0000001010101000b
dw 1000000111111110b
dw 0110000010000000b
dw 0010100001100000b
dw 0001111000101000b
dw 1000100010011110b
dw 0110011001101000b
dw 1010101010101110b
dw 0111111111111100b
dw 1110000000000001b
Листинг 6
псевдослучайная последовательность, записанная в виде 16-разрядных слов, отображаемых в двоичной нотации
Теперь определенная закономерность сразу же бросается в глаза (вот что значит правильно отформатировать листинг!). Биты каждого последующего элемента смещаются на одну позицию вправо, прижимаясь к логическому "востоку", образуя своеобразную битовую "струю", которая в своем диагональном течении линейно увеличивается в размерах (каждый последующий элемент добавляет ей еще один бит ширины), но на определенном этапе внезапно разбивается на ряд более мелких ручейков, причудливые переплетения которых образуют бессмысленную мешанину. Тем не менее, "физические" принципы, лежащие в основе этого "гидрологического" сооружения, все еще скрыты непроницаемой вуалью тумана и нам не остается ничего иного, кроме как брести наугад, полагаясь лишь на свою интуицию и удачу.
Что мы знаем? Немного… Скремблер выполняет операцию XOR[n2k47] "ксорит" над содержимымое своего внутреннего регистра ис потоком скремблируемых данных и после каждого "отскремблированного" 16-?разрядного слова модифицирует значение этого регистра… но вот как?! Давайте возьмем два соседних элемента нашей псевдослучайной последовательности и попробуем подобрать такую последовательность операций, которая из предыдущего элемента порождала бы следующий.
Возможных вариантов не так уж и много: сдвиг, XOR, AND и OR. Навряд ли создатели CD-?ROM использовали в скремблере что-то еще.
Итак, будет будем оттапливаетсяотталкиваться от того, что "Исаак родил Абрама", то есть от того как скремблер из числа 0110000000000000b скремблер неизвестным науке образом получил число 0010100000000000b. Для компенсации сдвига (который явно имел место) сместим последующий элемент на один бит влево и запишем оба числа одно под другим (по типу сложение по модулю два в столбик):
dw 011000000000000b
dw ???????????????b XOR
-------------------
dw 010100000000000b
Неизвестное слагаемое здесь не найдет только ленивый. Операция XOR над 011000000000000b [n2k48] и XOR 010100000000000b дает…001100000000000b. Постой! Но ведь это же наш исходный член, только сдвинутый на одну позицию вправо! Ну-ка, а как поведет себя следующая пара чисел? Сгорая от нетерпения складываем:
dw 010100000000000b
dw ???????????????b XOR
-------------------
dw 0001111000000000b
Ага, операция XOR над 010100000000000b и XOR 0001111000000000b дает 001010000000000b, значит, мы на верном пути! Наскоро написав простейший скрипит, вычисляющий последующие члены на основе предыдущих мы получим верный результат для всех членов последовательности со второго по седьмой включительно, а вот дальше… Дальше теория и практика разойдутся как большинство супругов. Неожиданно в старшем разряде возникнет единица, которую никто не ждал и которая, естественно, в следующей итерации порождает паразитный "ручеек". Может быть, сдвиг бит в слове происходит циклически, т. е. младший бит "заворачивается" наверх? Но нет, попытка вычисления последующихй членов не подтверждает этой теории.
Провозившись пару часов в попытках найти в доступной мне литературе хоть какую-то информацию о полиномах и особенностях их реализации, я так ни к чему и не пришел. В конце концов, вспоминиав, что "лучше за день долететь, чем за час добежать", я просто распечатал первую сотню членов псевдослучайной последовательности и вручную рассчитал каждый последующий элемент на основе предыдущего данного.
Затем просто отметил все обнаруженные исключения. Выяснилось, что 15-й и 14-й биты (считая от нуля) временами совершают "самопроизвольные" перескоки из нуля в единицу и наоборот. Остальные биты вели себя в полном соответствии с теорией.
Осталось всего ничего —– выяснить при каких условиях происходят эти битовые "мутации". Быстро обнаружилось, что если первый, считая от нуля, бит вычисленного члена последовательности равен единице, то его 15-й бит инвертируется (это действительно легко заметить, особенно если на распечатке). Чуть сложнее далось второе исключение из правил: если нулевой бит вычисленного члена равен единице, то его 15-й и 14-й биты инвертируетсяинвертируются. Соответственно, если и 0-й и 1-й биты содержат по единице, до в силу двойной инверсии 15-го бита реально инвертируется лишь 14-й бит (см. рис. 1.17 0х46). Все! Теперь мы можем рассчитать нашу псевдослучайную последовательность целиком!
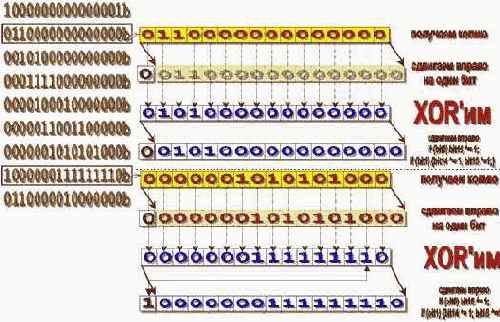
Рис. 1.17.унок 17 0x046 Расчет скремблируемой последовательности
Исходный текст программы, генерирующей скремблерную последовательность приведен в листинге 1.7ниже. Здесь и далее в квадратных скобках приведено название файла, находящегося на прилагаемом к книге компакт-диске с соответствующим листингом. Конечно, это далеко не верх оптимизации, но в плане наглядности данный пример весьма удачен.
Листинг 1.7. [/etc/RawScrambler.c] Программа для расчета скремблируемой последовательности
/*---------------------------------------------------------------------------
*
* ГЕНЕРИРУЕТ ПОСЛЕДОВАТЕЛЬНОСТЬ ДЛЯ CD-СКРЕМБЛЕРА
* ===============================================
*
* build 0x001 @ 07.06.2003
----------------------------------------------------------------------------*/
#include <stdio.h>
// контрольный фрагмент истинной последовательности для проверки программы
// -----------------------------------------------------------------------
//0x8001,0x6000,0x2800,0x1e00,0x0880,0x0660,0x02a8,0x81fe,0x6080,0x2860,0x1e28,
//0x889e,0x6668,0xaaae,0x7ffc,0xe001,0x4800,0x3600,0x1680,0x0ee0,0x04c8,0x8356,
//0xe17e,0x48e0,0x3648,0x96b6,0xeef6,0xccc6,0xd552,0x9ffd,0xa801,0x7e00,0x2080,
printf_bin(int a)
{
int b;
for(b = 15; b >= 0; b--) printf("%x",(a & (1<<b))?1:0);printf(" %x\n",a);
}
main()
{
int a, tmp;
int reg = 0x8001; // первый элемент скремблерной последовательности
for(a = 1; a < 1170/* длинна скремблируемой части сектора в словах*/; a++)
{
// вывод на печать
printf_bin(reg);
if ((a % 8) == 0) printf(".............%03d.................\n",a /8);
// сложение по модулю два со свдигом
tmp = reg >> 1; tmp = reg ^ tmp; reg = tmp >> 1;
// обработка полнинома x^15+x+1, что эквив. 1<<15 + 1<<1 + 1<<0
if (reg & 1<<1) reg = reg ^ (1<<15);
if (reg & 1<<0) reg = reg ^ ((1<<15) | (1<<14));
}
}
